Current project: Cuda optimized Monte Carlo algorithm applied to targeting and trajectory simulation of a parabolic laminar stream of water

Wow that was a mouth fulll.

Overview

The idea is that a water gun turret needs to be able to quickly identify it’s target and calculate the rotation toward, and elevation to it’s target. Really it's just an excuse to play with cuda and my ongoing water gun turret. 

Deeper

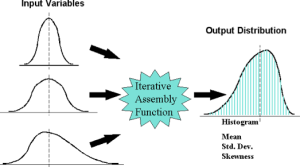
The program should accept a target position relative to the gun, with a known error range from the measurement device and quickly calculate the resulting water gun angle and elevation. The system will assume laminar flow and use known fluid dynamic models in trajectory calculations. A Monte Carlo algorithm will be applied to all variables in the calculations, such as crosswind, fore wind, ambient air pressure, internal system water pressure, Reynolds number, drag force, flow rates, and other variables. 

Each variable will have it’s own statical distribution, this will be identified ahead of time and included as input files. The Monte Carlo method requires that all the variables in the calculation be randomized according to their particular distribution, and inputed into the targeting function. This should result in a large number of calculated outputs. 

The resulting outputs will represent every possible outcome, with the more likely ones occurring more often. These outputs will be combined to generate a histogram of the final targeting solution. The targeting solution and the resulting histogram will be the final output of this program. 

Parallelization  

The main issue is that a single complex function is required to run many times with different data sets. This is an ideal problem to solve using the CUDA multicore architecture. 

validation

An expert has to verify my fluid dynamic function, and provide reasonable ranges and distribution for such variables such as resistance coefficient. I will run the same simulation experiment in MATHLAB, and in a serial version in C. The final CUDA code will be compared to the MATHLAB and C implementation. Because at no point will a runtime random number generator be used, the resulting output of both systems should always be deterministic and exactly the same for both systems.